\( \newcommand{\NOT}{\neg} \newcommand{\AND}{\wedge} \newcommand{\OR}{\vee} \newcommand{\XOR}{\oplus} \newcommand{\IMP}{\Rightarrow} \newcommand{\IFF}{\Leftrightarrow} \newcommand{\TRUE}{\text{True}\xspace} \newcommand{\FALSE}{\text{False}\xspace} \newcommand{\IN}{\,{\in}\,} \newcommand{\NOTIN}{\,{\notin}\,} \newcommand{\TO}{\rightarrow} \newcommand{\DIV}{\mid} \newcommand{\NDIV}{\nmid} \newcommand{\MOD}[1]{\pmod{#1}} \newcommand{\MODS}[1]{\ (\text{mod}\ #1)} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R} \newcommand{\C}{\mathbb C} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cL}{\mathcal L} \newcommand{\cK}{\mathcal K} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cZ}{\mathcal Z} \newcommand{\emp}{\emptyset} \newcommand{\bs}{\backslash} \newcommand{\floor}[1]{\left \lfloor #1 \right \rfloor} \newcommand{\ceil}[1]{\left \lceil #1 \right \rceil} \newcommand{\abs}[1]{\left | #1 \right |} \newcommand{\xspace}{} \newcommand{\proofheader}[1]{\underline{\textbf{#1}}} \)

CSC148 Assignment 2: Prefix Trees and Melodies

By this point in CSC148, we have studied several different abstract data types and data structures, and most recently looked at tree-based data structures that can be used to represent hierarchical data. On this assignment, you’ll explore a new tree-based data structure known as a prefix tree, which is a particular kind of tree used to store large quantities of data organized into a hierarchy by common “prefixes”.

You’ll first implement this new data structure and then apply it to a few different problem domains, one of which is a text-based autocompletion tool similar to what online search engines like Google use.

Screenshot of Google search with autocomplete.

Logistics

Starter files

To obtain the starter files for this assignment:

  1. Login to MarkUs and go to CSC148.
  2. Under the list of assignments, click on Assignment 2.
  3. To access the starter files, you’ll first need to either create a group or indicate you are working individually. You can change this later if you decide to partner with another student.
  4. Then, click on the Download Starter Files button (near the bottom of the page). This will download a zip file to your computer.
  5. Extract the contents of this zip file into your csc148/assignments/a2 folder.
  6. You can then open these files in your PyCharm csc148 project, just like all of your other course materials.

General instructions

This assignment contains a series of programming tasks to complete. This is similar in structure to the Weekly Preparation Synthesize exercises, but more complex. Your programming work should be completed in the different starter files provided (each part has its own starter file). We have provided code at the bottom of each file for running doctest examples and PythonTA on each file.

Like the prep exercises, this assignment will be automatically graded using a combination of test cases to check the correctness of your work and PythonTA to check the code style and design elements of your work.

The problem domain: autocompleters and prefix trees

Please begin by reading the following textbox to learn about the main new abstract data type and data structure you’ll work with for this assignment.

The Autocompleter ADT

The Autocompleter abstract data type (ADT) stores a collection of values, where each value has an associated weight (a positive number). Any type of value can be stored in an Autocompleter.

When we store a value, we must specify not just the value and its weight, but also an associated list called the prefix sequence of the value. The form of these prefix sequences depends on how we want to use the Autocompleter. Here are some examples:

The Autocompleter ADT itself does not specify how these prefix sequences are chosen, just as how a Python dict doesn’t care about the type of its keys or values. As we’ll see on this assignment, different client code will use different types of values and prefix sequences depending on its goals.

Autocompleter operations

The Autocompleter ADT supports the following operations:

It is mainly the autocomplete operation that distinguishes this abstract data type from Python’s built-in lists and dictionaries. Both the autocomplete and remove operations accept a list as a input prefix. We say that a value in the Autocompleter matches the given list as a prefix if the prefix sequence used to insert the value starts with the same elements as the input prefix. (In Python, we can write “lst1 starts with the elements of lst2” with the expression lst1[0:len(lst2)] == lst2.)

So unlike the regular Set ADT, which supports searching for a specific value (i.e., __contains__), an Autocompleter allows the user to search for multiple values at once by specifying a prefix that matches multiple values. For example, suppose we have a prefix tree with the following values and prefix sequences inserted:

Then if we perform an autocomplete operation with the prefix ['c', 'a'], we expect to retrieve the values 'cat' and 'care'.

Note: the empty list is a prefix of every Python list, and so we can perform an autocomplete operation with the input prefix [] to obtain all values stored in the Autocompleter.

Limiting autocomplete results

For very large datasets, we usually don’t want to see all autocomplete results (think, for example, about Google’s autocompletion when you start typing a few letters into its search box). Because of this, the autocomplete operation takes an optional positive integer argument that specifies the number of matching values to return. If the number of matches is less than or equal to the limit, all of the matches are returned.

When the number of matching values exceeds the given limit, how does the Autocompleter choose which values to return? This is where the weights come in, but not how you might expect. We will NOT simply return the matching values with the largest weights—doing so is tricky to do efficiently! Instead, in Part 2 of this assignment you’ll implement an autocompletion operation that will take weights into account, but in a limited way.

The prefix tree data structure

There are many ways you could implement the Autocompleter ADT using what you’ve learned so far. You might, for example, store each value, weight, and prefix sequence in a list of tuples, and then iterate through the entire list in each autocomplete operation. This approach has the downside that every single tuple would need to be checked for each autocomplete (or remove) operation, even if only a few tuples match the given prefix.

To support the required operations in an efficient manner, we will use a tree-based data structure called a simple prefix tree. Here is the main idea for this data structure:

Example simple prefix tree

This is a bit abstract, so let’s look an example. Suppose we want to store these strings:

'car', 'cat', 'care', 'dog', 'danger'

We want to autocomplete on these strings by individual letters, and so a prefix sequence for each string is simply a list of the individual characters of each string. For example, the prefix sequence for 'car' is ['c', 'a', 'r'].

Here is a simple prefix tree for these five strings (we’ve omitted quotation marks and weight values):

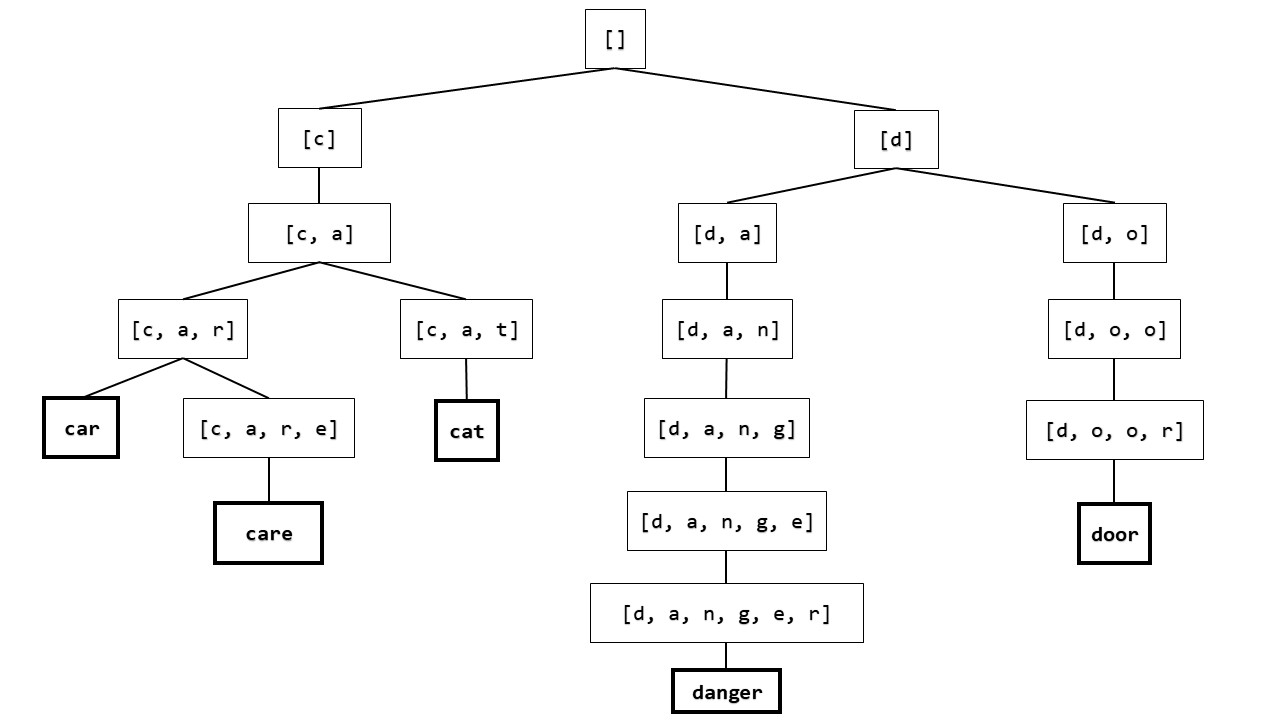
The root of the tree is [], the common prefix for all strings in the tree. The root has two children, with values ['c'] and ['d'], which divides the words into two groups based on their common first letters. Each subtree then is further subdivided by longer and longer prefixes, until finally each leaf stores one of the five original strings. Pay attention to types here: in this simple prefix tree, each internal value is a list of strings that represents a prefix, and each leaf value is a single string, which is the original value the prefix tree stores.

As we mentioned above, there is a straightforward parent-child relationship between internal values: each prefix in a parent is extended by one element to obtain the prefix in the child. This makes the overall tree structure very predictable, and in particular, the path from the root to a leaf contains all the prefixes of the leaf value’s prefix sequence, in increasing order of prefix length.

You might notice that many of these internal values seem redundant, as they trace out just a single path to a leaf (e.g., 'danger'). This is why we call this kind of prefix tree a simple prefix tree: its structure is very predictable, but also wasteful in terms of the overall tree size. We’ll address this limitation in the last part of this assignment.

Prefix tree weights

The last concept to cover is how prefix trees store the weights of the values that have been inserted. This is done as follows:

For reasons that will become clear in Part 2 of this assignment, every list of subtrees must be sorted in non-increasing order of weight.

Part 1: Beginning with SimplePrefixTree

Your first task will be to get familiar with the main classes you’ll use on this assignment. Open a2_prefix_tree.py and read through the provided starter code for the Autocompleter and SimplePrefixTree classes (ignore CompressedPrefixTree for now).

Part (a): Simple tree methods

Make sure you review all of the starter code carefully. In particular, pay attention to SimplePrefixTree’s four three attributes and all of the representation invariants.

Then when you are ready, implement the first four methods __init__, __len__, is_empty, is_leaf, and __len__. For is_empty and is_leaf, you’ll need to read the documentation carefully to determine how to tell if a SimplePrefixTree is empty or a leaf.

Part (b): Insertion warmup (not to be handed in)

In Part (c) below, you’ll implement the first key method of SimplePrefixTree, insert. This involves a more complex version of the Tree insertion method you implemented in Lab 8. So to warmup, we encourage you to open a2_part1b.py and implement the Tree.insert_repeat method according to its docstring.

This exercise is optional (and not to be handed in), but we strongly suggest completing it and making sure your implementation passes all of the provided doctests (and any other tests that you add) before moving onto Part 1(c).

Part (c): Insertion

Next, implement SimplePrefixTree.insert—we haven’t provided a method header, but pay attention to the inheritance relationship! This should tell you where to find the specification for this method.

This method must be implemented recursively, and be aware that you’ll need to create new SimplePrefixTree objects to represent the different prefixes as you go down the tree. We strongly recommend completing Part (b) before attempting this part.

Check your work!

We want you to start thinking about generating good test cases even at this point. We have provided some basic in a2_sample_test.py for this part and for the rest of this assignment. Here are some ideas for more specific test cases to add to that file:

Part 2: Implementing autocompletion

Now that you are able to insert values into a prefix tree, next step is to implement autocompletion (the autocomplete method). You should do this in two parts:

  1. First, implement an unlimited autocomplete, where you ignore the limit parameter and always return every value that matches the input prefix.

  2. Then, implement the limited autocomplete, using the algorithm described in the box below.

    Limited autocomplete, greedy algorithm

    The algorithm for a weight-based limited autocomplete is the following:

    1. For each subtree in non-increasing weight order, obtain any autocomplete results for the given prefix (this is a recursive call), and add the results to a list accumulator. Pass in the appropriate limit argument to recursive calls so that no “extra” values are returned.
    2. Repeat Step 1 until the accumulator’s length reaches the target limit. When it does, stop immediately and return it, without checking any other subtrees.

    Why “greedy”?

    Because each tree’s weight is equal to the sum of the weights of its subtrees, this algorithm isn’t guaranteed to return the matching leaf values with the largest weights. Suppose, for example, we have a SimplePrefixTree with two subtrees, where the first subtree has 100 leaf values, each with weight 1.0, and the second subtree has a single leaf with weight 50. Then the first subtree has a weight of 100, and this algorithm will accumulate leaves from that subtree before getting to the second subtree.

    This behaviour may seem counter-intuitive, but is an example of an algorithm that trades off precision for efficiency. Rather than retrieving all matching leaves and then sorting them by weight, this algorithm will only retrieve up to limit leaves, which may be much smaller than the total number of leaves in the tree. We call it a “greedy” algorithm because it makes short-sighted choices based on the subtree weights, without knowing about the actual leaf values stored.

Note that because of the SimplePrefixTree representation invariants, each subtree list should already be sorted in non-increasing weight order when you call autocomplete; don’t re-sort the subtrees inside autocomplete, as this will make your code very inefficient. (If you find the subtrees aren’t sorted by weight correctly, go back to your insert implementation!)

Check your work!

At this point, you should try inserting some values into a prefix tree, and then calling autocomplete to obtain some results. Here are some suggestions of input properties/conditions to help you design test cases (add to this!):

Part 3: Implementing removal

Your task in this section is to implement the SimplePrefixTree.remove method. The recursive structure is similar to SimplePrefixTree.autocomplete, but since this is a mutating operation, you’ll need to be careful about preserving all representation invariants (e.g., updating weights, making sure there aren’t any empty subtrees1).

Warning: our notion of “empty subtree” for prefix trees is subtly different from the Tree class from lecture. A prefix tree should be empty if it no longer stores any leaf values that were previously inserted.

Here is an example that illustrates this.

>>> prefix_tree = SimplePrefixTree()
>>> prefix_tree.insert('cat', 1.0, ['c', 'a', 't'])
>>> prefix_tree.insert('car', 1.0, ['c', 'a', 'r'])
>>> prefix_tree.remove(['c', 'a'])  # This removes both values that were inserted
>>> prefix_tree.is_empty()  # The tree should now be EMPTY
True
>>> prefix_tree.subtrees  # More explicitly, it should no longer have any subtrees
[]

Check your work!

We strongly recommend starting with very small trees containing just a few values, and then deleting one value at a time and checking at each step that the resulting tree has the right structure and weights.

After finishing this part, you should have a complete SimplePrefixTree class. Onto some fun applications!

Part 4: Text-based autocompletion

Next, open a2_autocomplete_engines.py. Inside are the start of two classes LetterAutocompleteEngine and SentenceAutocompleteEngine. Both of them are relatively simple classes that use an Autocompleter to perform some autocomplete actions. Both classes store strings as the values in their Autocompleter, but differ in how they generate prefix sequences for each string.

Note that the LetterAutocompleteEngine can also take a string with spaces in it, and each space is treated just like any other letter. For example, the string 'how are' would have the prefix sequence ['h', 'o', 'w', ' ', 'a', 'r', 'e'].

Your task is to complete the implementation of these two classes based on their specification and the implementation instructions in the starter code. The hardest part of each class is their initializer; the other methods should be simple calls to methods you implemented in previous parts.

Note: you’ll see the initializer docstrings mention the configuration key 'autocompleter'. For now, you can assume that this key’s value will always be 'simple', which corresponds to the SimplePrefixTree class from Parts 1-3. You’ll add to this in Part 6.

Text sanitization

Both LetterAutocompleteEngine and SentenceAutocompleteEngine will read data from a file to populate their Autocompleters. Real world data is often messy, and we often sanitize (or clean) the data before using them in the rest of our program.

You are responsible for performing two sanitization operations for any text from files given to these classes:

  1. Convert all letters to lowercase.
  2. Remove any characters that are not alphanumeric and not space (' ') characters. In other words, keep only alphanumeric and space characters. Remove other forms of whitespace, such as the newline character '\n'.

This sanitization should be done before inserting into an Autocompleter. This means that your Autocompleters for these classes should only ever receive lowercase letters, numbers, and whitespace in both the prefixes and the string values at the leaves. It also means that two different strings in the input data can be sanitized to the same string! For example, the strings 'The', 'the', and even 'THE?!?!' would all be sanitized to the same string 'the' before being added to the Autocompleter.

Hint: look up Python’s string methods and you should find some that are useful.

Check your work!

At the bottom of a2_autocomplete_engines.py, we’ve provided some functions to illustrate a sample run of each engine. We have also provided a sample test in a2_sample_test.py. As in previous assignments, we strongly recommend that you try creating your own small dataset files yourself, as this will make it easier to test different cases, including duplicate lines.

Part 5: Let’s make some music 🎵

Our last Autocompleter application will be a fun one: performing autocompletion on song melodies! First, some background definitions.

Musical definitions

A note represents a single sound. In Python, we represent a note as a tuple[int, int], where the first integer represents the pitch of the note,2 and the second represents its duration in milliseconds. A melody is a sequence of one or more notes. In a2_melody.py, we’ve defined a Melody class that stores a list of notes and a name for the melody.

An interval is the difference in pitch between two notes. And finally, the interval sequence of a melody is a list containing the differences between consecutive notes in the melody. For example, if a melody contains the sequence of notes

[(59, 300), (41, 300), (45, 600), (40, 600), (40, 600)]

then its corresponding interval sequence is [-18, 4, -5, 0].

Your task is to complete the MelodyAutocompleteEngine class; as in the previous part, the hardest part is the initializer. You may not modify the a2_melody.py starter file. So if you want to write helper functions related to Melody objects, you should define top-level functions in a2_autocomplete_engines.py rather than add new Melody methods.

Part 6: Compressing prefix trees

You might have noticed that SimplePrefixTree is somehwat inefficient: because we require that every internal value be a list that’s only one element longer than its parent, it is possible to get very long paths down a simple prefix tree that lead to just a single value. You can see a small example of this in the diagram of the simple prefix tree earlier in the handout with the path leading to the word 'danger'. Let’s now formalize this type of “inefficiency”.

Compressing prefix trees

We say that an internal value in a prefix tree is compressible if it has exactly one child, and that child is also an internal value. Equivalently, we say that an internal value is incompressible if it has more than one child or it is the parent of a leaf.

We say that a prefix tree is fully compressed when it has no compressible internal values. An empty prefix tree is fully compressed.

For example, here is a fully compressed version of the prefix tree from the start of the handout.

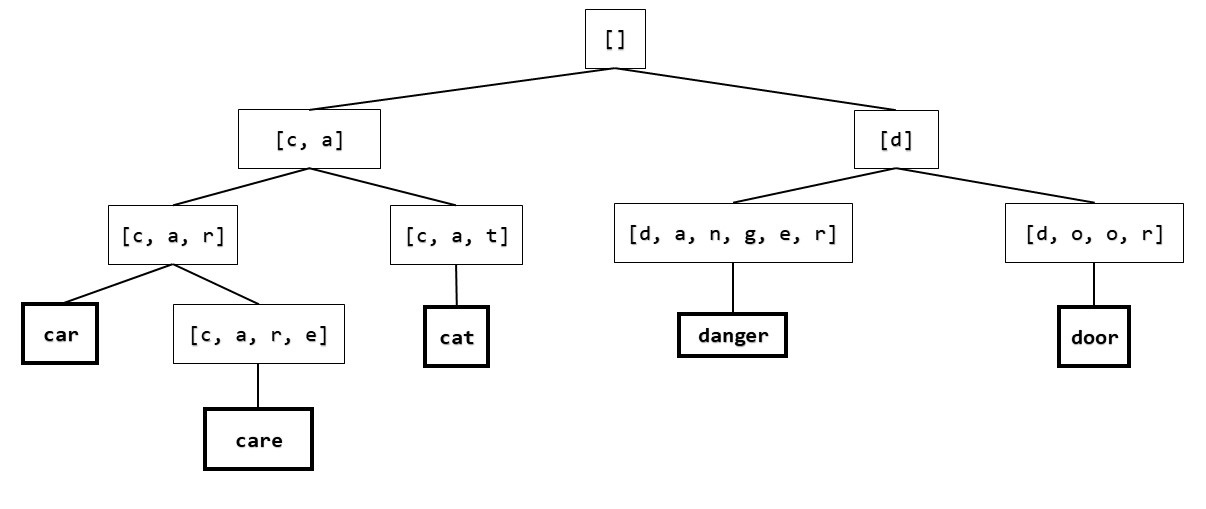
Compressed prefix tree.

Intuitively, fully compressed prefix trees still contain the same information as the simple prefix trees we studied earlier on this assignment, but they have the potential to implement the Autocompleter operations more efficiently, since (intuitively) fewer recursive calls need to be made to reach the leaves of the tree.

Your final task for this assignment is in a2_prefix_tree.py: implement the class CompressedPrefixTree, which has the same public interface (attributes and methods, including the initializer) as SimplePrefixTree, except that it has different representation invariants:

You’ll also need to update the initializers for the three “autocomplete engine” classes to make sure to use the CompressedPrefixTree when given the configuration value 'autocompleter': 'compressed'.

This part is the most algorithmically challenging part of any assignment in this course! To help you get started, here are two different strategies you might use to implement the CompressedPrefixTree.insert method.

Finally, if you get stuck, we strongly recommend making sure you’ve completed and tested the rest of this assignment before spending all of your remaining time on this part of the assignment.

Check your work!

After you complete this task, you should be able to run your existing tests for SimplePrefixTree on your new class CompressedPrefixTree, since they have the same public interface (right?!). For the same reason, you should be able to use both kinds of prefix trees in your autocompletion engines in Parts 4 and 5 (change the 'autocompleter' configuration value).

Submission instructions

Before submitting your work, please do the following:

  1. Make sure you can run every assignment file. As we explain in Running and Testing Your Code Before Submission, it is essential that your submitted code not contain syntax errors. Python files that contain syntax errors will receive a grade of 0 on all grading involving those files. You have lots of time to work on this assignment and check that each file runs (e.g., right-click -> “Run in Python Console”), so please make sure to do this regularly and fix syntax errors right away. Remember, this doesn’t mean you need to have completed the whole assignment! You can still get lots of partial credit for the work you complete as long as your code can be run by Python.
  2. Run your tests one last time (both doctests and pytest). This will help catch any “last-minute changes” that might accidentally have introduced a bug into your code.
  3. In each module, run the provided python_ta.check_all() code to check for PythonTA errors, and fix them! Tip: most formatting errors (e.g., blank lines, whitespace) can be fixed automatically in PyCharm by using the menu option Code -> Reformat Code.
  4. Remove any code you added just for debugging, such as print function calls. Remove any large blocks of commented-out code. If you want to save an old or alternate approach, create a copy of the file instead.
  5. Take pride in your beautiful code. 😎

Now, to actually submit your work:

  1. Login to MarkUs.

  2. Go to Assignment 2, then the “Submissions” tab.

  3. If you are working with a partner, make sure you have formed a group on MarkUs.

  4. Submit the following files: a2_autocomplete_engines.py and a2_prefix_tree.py. Do not submit any other files. Please note that MarkUs is picky with filenames, and so your filenames must match these exactly, including using lowercase letters.

    Tip: you can select multiple files at once for submission.

    If you are working with a partner, only one of you needs to submit the files.

  5. Refresh the page, and then download each file to make sure you submitted the right version.

Remember, you can submit your files multiple times before the due date. So you can aim to submit your work early, and if you find an error or a place to improve before the due date, you can still make your changes and resubmit your files.

Congratulations, you are now finished with your final assignment in CSC148. Go do something fun, have some chocolate, or do a cartwheel to celebrate! 😎

Image of a dog wearning sunglasses. Source: https://www.ndtv.com/offbeat/some-dogs-out-there-uk-veterinarian-on-dogs-wearing-sunglasses-3029847

  1. You may find it helpful to review the discussion of handling empty subtrees in Section 8.3 of the Course Notes.↩︎

  2. You can find a chart showing the conversion between integers and standard note names here.↩︎