17.2 Some Properties of Graphs

In the previous section, we learned about the graph data type, and various pieces of terminology associated with graphs. Now that we have these definitions in hand, in this section we’ll cover a few basic proofs of some key properties of graphs. The proofs in this section will illustrate a few different proof techniques that we can use on graphs; these techniques will be ones that you’ve studied before, now applied to this new context.

The maximum number of edges in a graph

Here is our first “universal proof” on graphs: a statement about the maximum possible number of edges a graph can have.

Prove that for all graphs $G = (V, E)$, $|E| \leq \frac{|V|(|V|-1)}{2}$.

The statement we’re proving universially quantifies $G$. Since how we declare a graph variable looks syntactically different (“$G = (V, E)$”) than declaring a numeric variable, we’ll adopt an assumed domain of “set of all graphs” for the rest of this chapter rather than introducing a “set of all graphs” explicitly. \[\forall G = (V, E),~ |E| \leq \frac{|V|(|V| - 1)}{2}.\] Note that the structure of the statement is pretty straightforward, with the only tricky bit being that $G$ is not an arbitrary number, but an arbitrary graph.

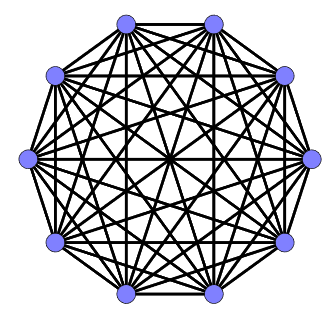
A graph with all possible edges.

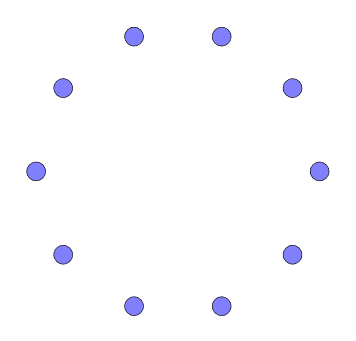
A graph with no edges.

So I’m trying to prove a relationship between the number of edges and vertices in any possible graph. I can’t assume anything about the structure of the graph: it could have any number of vertices and edges, and this property should still hold.

It turns out that we can use induction to prove statements about graphs. But in order to do so, we’ll need to introduce a new variable that’s a natural number, so that the statement we’re proving has the form $\forall n \in \N,~ P(n)$. A typical strategy for graphs is to introduce a variable representing the number of vertices (i.e., $n = |V|$). Here is the statement we’ll actually prove:

\[ \forall n \in \N,~ \forall G = (V, E),~ |V| = n \Rightarrow |E| \leq \frac{n(n - 1)}{2} \]

We’ll prove this statement by induction on $n$. Our predicate is:

\[ P(n): \forall G = (V, E),~ |V| = n \Rightarrow |E| \leq \frac{n(n - 1)}{2} \quad\quad \text{where $n \in \N$} \]

Or in English, $P(n)$ means “For all graphs $G$, if $G$ has $n$ vertices then it has at most $\frac{n(n-1)}{2}$ edges.

Base case: let $n = 0$. We need to prove $P(0)$.

Let $G = (V, E)$ be an arbitrary graph, and assume that $|V| = 0$. In this case, the graph has no vertices, and so cannot have any edges. Therefore $|E| = 0$, and satisfies the inequality $|E| \leq \frac{0 (0 - 1)}{2}$.

Induction step: let $k \in \N$ and assume that $P(k)$ holds: every graph with $k$ vertices has at most $\frac{k(k - 1)}{2}$ edges. We need to prove $P(k + 1)$.

Let $G = (V, E)$ be an arbitrary graph, and assume that $|V| = k + 1$. We want to prove that $|E| \leq \frac{(k + 1)k}{2}$.

Let $v$ be a vertex in $V$.$v$ here is arbitrary: it doesn’t matter which vertex we pick. We can divide the edges of $G$ into two groups:

$E_1$, the set of edges that contain $v$. Since there are $k$ other vertices in $V$ that $v$ could be adjacent to, $|E_1| \leq k$.
$E_2$, the set of edges that do not contain $v$. To count these edges, suppose we remove $v$ from the graph $G$, to obtain a new graph $G'$. Then $E_2$ is exactly the set of edges of $G'$.

But since $G'$ has one fewer vertex than $G$, we know $G'$ has $k$ vertices. By the induction hypothesis, we know that $G'$ has at most $\frac{k(k-1)}{2}$ edges, so $|E_2| \leq \frac{k(k-1)}{2}$.

Putting this together, we have: \[\begin{align*} |E| &= |E_1| + |E_2| \\ &\leq k + \frac{k(k-1)}{2} \\ &= \frac{(k+1)k}{2} \end{align*}\]

The transitivity of connectedness

Recall that we say two vertices in a graph are connected when there exists a path between them. Now let us look at one extremely useful property of connectedness: the fact that if two vertices in a graph are both connected to a third vertex, then they are also connected to each other.

Let $G = (V, E)$ be a graph, and let $u, v, w \in V$. If $v$ is connected to both $u$ and $w$, then $u$ and $w$ are connected.In mathematical terms, we say that vertex-connectedness is a transitive property.

Once again, after we get over the fact that we are quantifying over the set of all possible graphs, the translation is pretty straightforward, as the statement’s structure is not that complex. To make the formula even more concise, we’ll use the predicate $Conn(G, u, v)$ to mean that “$u$ and $v$ are connected vertices in $G$”.

\[\forall G = (V, E),~ \forall u, v, w \in V,~ \big(Conn(G, u, v) \land Conn(G, v, w) \big) \Rightarrow Conn(G, u, w).\]

Let’s examine the structure of the statement first. We have an arbitrary graph and three vertices in that graph. Because we’re proving an implication, we assume its hypothesis: that $u$ and $v$ are connected, and that $v$ and $w$ are connected. We need to prove that $u$ and $w$ are also connected.

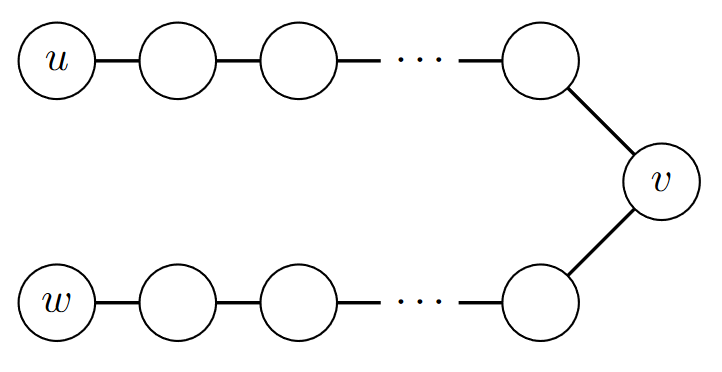
Let’s rephrase that by unpacking the definition of “connected.” We can assume that there is a path between $u$ and $v$, and between $v$ and $w$. We need to prove that there is a path between $u$ and $w$. Phrased that way, it may seem obvious what to do: create a path between $u$ and $w$ by joining the path between $u$ and $v$ and the one between $v$ and $w$.

There’s only one problem with this: the paths between $u$ and $v$ and $v$ and $w$ might contain some vertices in common, and paths are not allowed to have duplicate vertices. We can fix this, however, by using a simple idea: find the first point of intersection between the paths, and join them at that vertex instead.

Let $G = (V, E)$ be a graph, and $u, v, w \in V$. Assume that $u$ and $v$ are connected, and $v$ and $w$ are connected. We want to prove that $u$ and $w$ are connected.

Let $P_1$ be a path between $u$ and $v$, and $P_2$ be a path between $v$ and $w$. (By the definition of connectedness, both of these paths must exist.)

Image of paths from u to v and w to v.

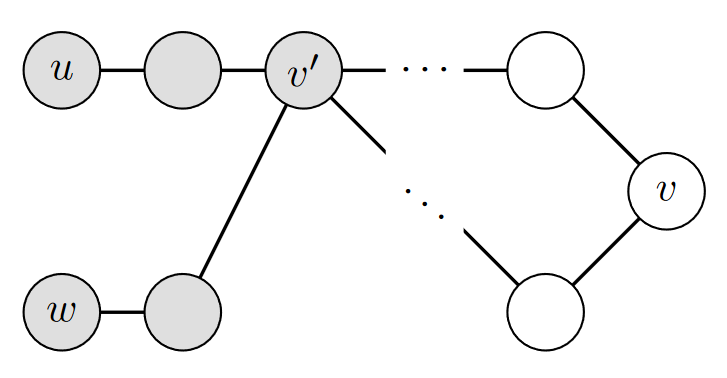
Handling multiple shared vertices: Let $S \subseteq V$ be the set of all vertices which appear on both $P_1$ and $P_2$. Note that this set is not empty, because $v \in S$. Let $v'$ be the vertex in $S$ which is closest to $u$ in $P_1$. This means that no vertex in $P_1$ between $u$ and $v'$ is in $S$, or in other words, is also on $P_2$.

Finally, let $P_3$ be the path formed by taking the vertices in $P_1$ from $u$ to $v'$, and then the vertices in $P_2$ from $v'$ to $w$. Then $P_3$ has no duplicate vertices, and is indeed a path between $u$ and $w$. By the definition of connectedness, this means that $u$ and $w$ are connected.

A proof by contradiction

Our final example in this section is one somewhat surprising property of graphs, and is a great illustration of the technique of proof by contradiction.

Prove that for all graphs $G = (V, E)$, if $|V| \geq 2$ then there exist two vertices in $V$ that have the same degree. Recall that the degree of a vertex is its number of neighbours.

$\forall G = (V, E),~ |V| \geq 2 \Rightarrow \big(\exists v_1, v_2 \in V,~ d(v_1) = d(v_2) \big)$

Assume for a contradiction that this statement is False, i.e., that there exists a graph $G = (V, E)$ such that $|V| \geq 2$ and all of the vertices in $V$ have a different degree. We’ll derive a contradiction from this. We also let $n = |V|$.

First, let $v$ be an arbitrary vertex in $V$. We know that $d(v) \geq 0$, and because there are $n - 1$ other vertices not equal to $v$ that could be potential neighbours of $v$, $d(v) \leq n - 1$. So every vertex in $V$ has degree between 0 and $n-1$, inclusive.

Since there are $n$ different vertices in $V$ and each has a different degree, this means that every number in $\{0, 1, \dots, n-1\}$ must be the degree of some vertex (note that this set has size $n$). In particular, there exists a vertex $v_1 \in V$ such that $d(v_1) = 0$, and another vertex $v_2 \in V$ such that $d(v_2) = n-1$.

Then on the one hand, since $d(v_1) = 0$, it is not adjacent to any other vertex, and so $\{v_1, v_2\} \notin E$.

But on the other hand, since $d(v_2) = n-1$, it is adjacent to every other vertex, and so $\{v_1, v_2\} \in E$.

So both $\{v_1, v_2\} \notin E$ and $\{v_1, v_2\} \in E$ are True, which gives us our contradiction!