15.1 Introduction to Trees

\( \newcommand{\NOT}{\neg} \newcommand{\AND}{\wedge} \newcommand{\OR}{\vee} \newcommand{\XOR}{\oplus} \newcommand{\IMP}{\Rightarrow} \newcommand{\IFF}{\Leftrightarrow} \newcommand{\TRUE}{\text{True}\xspace} \newcommand{\FALSE}{\text{False}\xspace} \newcommand{\IN}{\,{\in}\,} \newcommand{\NOTIN}{\,{\notin}\,} \newcommand{\TO}{\rightarrow} \newcommand{\DIV}{\mid} \newcommand{\NDIV}{\nmid} \newcommand{\MOD}[1]{\pmod{#1}} \newcommand{\MODS}[1]{\ (\text{mod}\ #1)} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R} \newcommand{\C}{\mathbb C} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cL}{\mathcal L} \newcommand{\cK}{\mathcal K} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cZ}{\mathcal Z} \newcommand{\emp}{\emptyset} \newcommand{\bs}{\backslash} \newcommand{\floor}[1]{\left \lfloor #1 \right \rfloor} \newcommand{\ceil}[1]{\left \lceil #1 \right \rceil} \newcommand{\abs}[1]{\left | #1 \right |} \newcommand{\xspace}{} \newcommand{\proofheader}[1]{\underline{\textbf{#1}}} \)

While the List abstract data type is extremely common and useful, not all data has a natural linear order. Family trees, corporate organization charts, classification schemes like “Kingdom, Phylum, etc.” and even file storage on computers all follow a hierarchical structure, in which each entity is linked to multiple entities “below” it.

Tree definition and terminology

In computer science, we use a tree data structure to represent this type of hierarchical data. Trees are a recursive data structure, with the following recursive definition. A tree is either:

empty, or
has a root value connected to any number of other trees, called the subtrees of the tree. One quirk of our definition is that subtrees are allowed to be empty. We almost exclusively work with non-empty trees when representing real-world data, but there are some cases when allowing empty subtrees is useful or necessary. We’ll explore this in one such application later this chapter.

We generally draw the root at the top of the tree; the rest of the tree consists of subtrees that are attached to the root. Note that a tree can contain a root value but not have any subtrees: this occurs in a tree that contains just a single item. For example, the root value of the tree below is labeled A; the root is connected to three subtrees. Because subtrees are themselves trees, each one has its own subtrees. This sometimes leads to confusion! The term “subtree” is always relative to an outer tree, where each subtree is connected to the root of that outer tree.

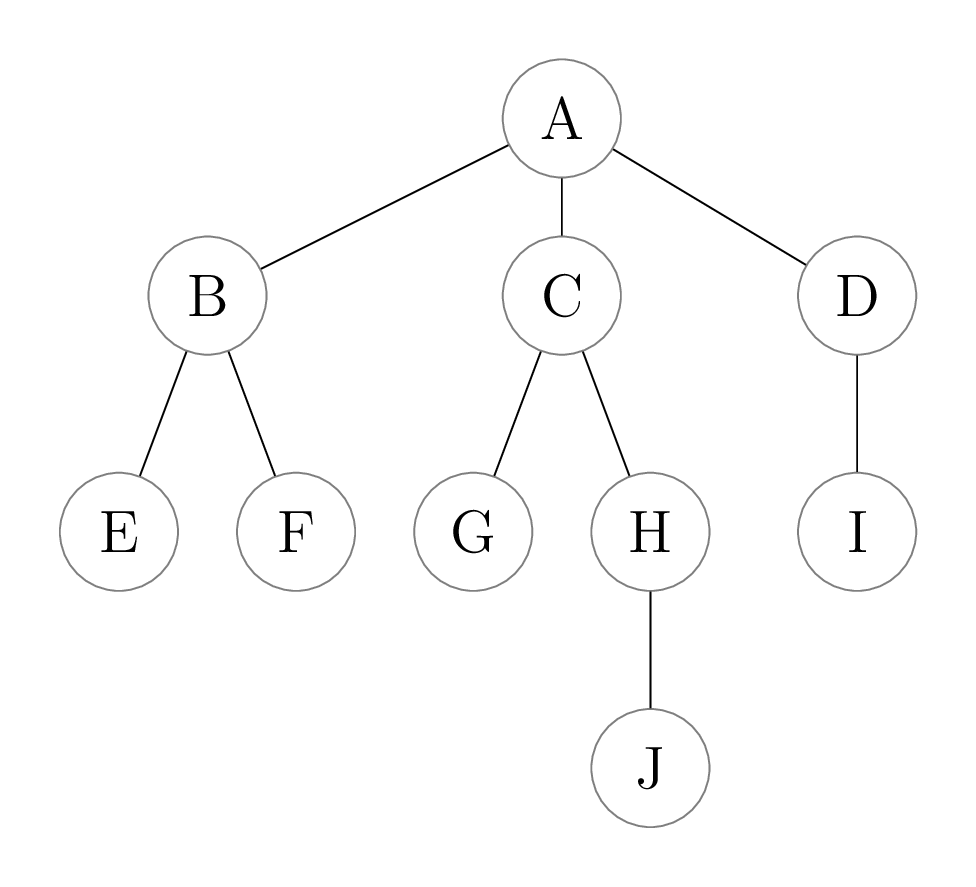
Tree diagram

The size of a tree is the number of values in the tree. The size of the above tree is 10. What’s the relationship between the size of a tree and the size of its subtrees?

A leaf is a value with no subtrees. The leaves of the above tree are labeled E, F, G, J, and I. What’s the relationship between the number of leaves of a tree and the number of leaves of its subtrees?

The opposite of a leaf is an internal value, which is a value that has at least one subtree. The internal values of the above tree are labeled A, B, C, D, and H. What’s the relationship between the number of internal values of a tree and the number of leaves of its subtrees?

The height of a tree is the length of the longest path from its root to one of its leaves, counting the number of values on the path. The height of the above tree is 4. What’s the relationship between the height of a tree and the heights of its subtrees?

The children of a value are all values directly connected underneath that value. The children of A are B, C, and D. Note that the number of children of the root of a tree is equal to the number of its subtrees, but that these two concepts are quite different. The descendants of a value are its children, the children of its children, etc. This can be defined recursively as “the descendants of a value are its children, and the descendants of its children.” What’s the relationship between the number of descendants of a value and the number of descendants of its children?

Similarly, the parent of a value is the value immediately above and connected to it; each value in a tree has exactly one parent, except the root, which has no parent. The ancestors of a value are its parent, the parent of its parent, etc. This too can be defined recursively: “the ancestors of a value are its parent, and the ancestors of its parent.”

Note: sometimes, it will be convenient to say that descendants/ancestors of a value include the value itself; we’ll make it explicit whether to include the value or not when it comes up. However, a value is never a child or parent of itself.

A tree implementation

Here is a simple implementation of a tree in Python. As we did with linked lists, we’ll start with a very simple implementation and then develop additional methods throughout this chapter.

from __future__ import annotations
from typing import Any, Optional


class Tree:
    """A recursive tree data structure.

    Representation Invariants:
        - self._root is not None or self._subtrees == []
    """
    # Private Instance Attributes:
    #   - _root:
    #       The item stored at this tree's root, or None if the tree is empty.
    #   - _subtrees:
    #       The list of subtrees of this tree. This attribute is empty when
    #       self._root is None (representing an empty tree). However, this attribute
    #       may be empty when self._root is not None, which represents a tree consisting
    #       of just one item.
    _root: Optional[Any]
    _subtrees: list[Tree]

    def __init__(self, root: Optional[Any], subtrees: list[Tree]) -> None:
        """Initialize a new Tree with the given root value and subtrees.

        If root is None, the tree is empty.

        Preconditions:
            - root is not none or subtrees == []
        """
        self._root = root
        self._subtrees = subtrees

    def is_empty(self) -> bool:
        """Return whether this tree is empty.
        """
        return self._root is None

Our Tree initializer creates either an empty tree (when root is None), or a tree with a root value and the given subtrees. Note that it is possible for root to not be None, but subtrees to still be empty: this represents a tree with a single root value, and no subtrees. As we’ll see in the next section, the empty tree and single value cases are generally the base cases when writing recursive code that operates on trees.