
A fractal is a geometric figure that has been defined recursively: i.e., a figure that can be split into parts, each of which is a smaller copy of the original. In this section, we’ll study one of the most famous fractals, the Sierpinski Triangle, and use the power of recursion to draw the Sierpinski triangle in Python.
The Sierpinski Triangle
The Sierpinski Triangle has the shape of an equilateral triangle, which has been subdivided into four smaller and congruent equilateral triangles. The smaller triangle in the centre is “empty”, while the remaining three smaller triangles are themselves smaller Sierpinski Triangles.
We can draw a Sierpinski Triangle as follows:
Draw a large equilateral triangle.

Divide this triangle into four smaller triangles by connecting the midpoints of each side of the triangle.
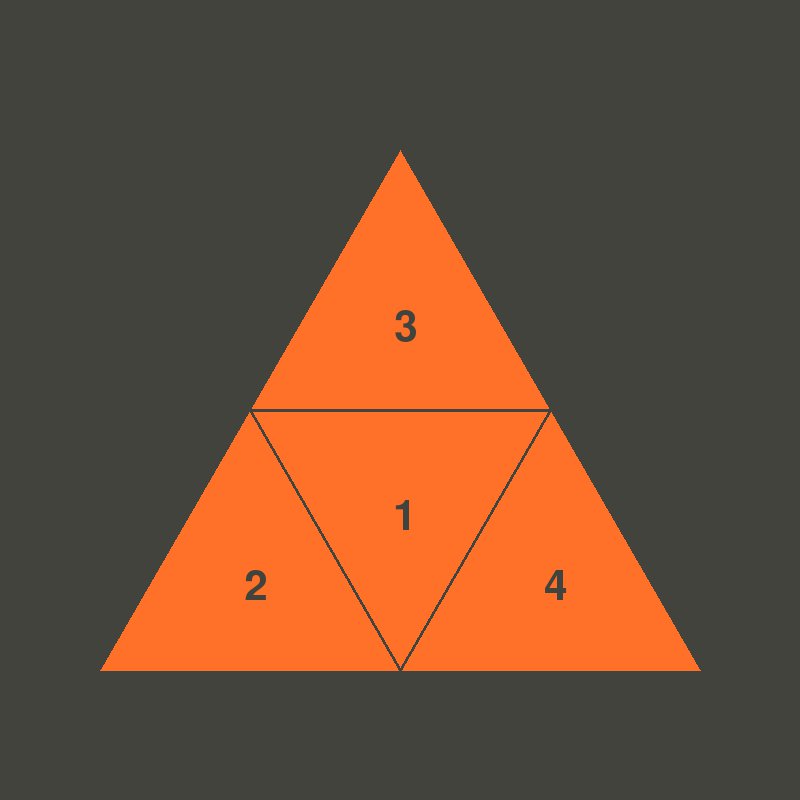
Fill the smaller triangle in the centre with “negative space” (i.e. fill it with the colour of the background).

Repeat steps 2-3 on each of the remaining smaller triangles.
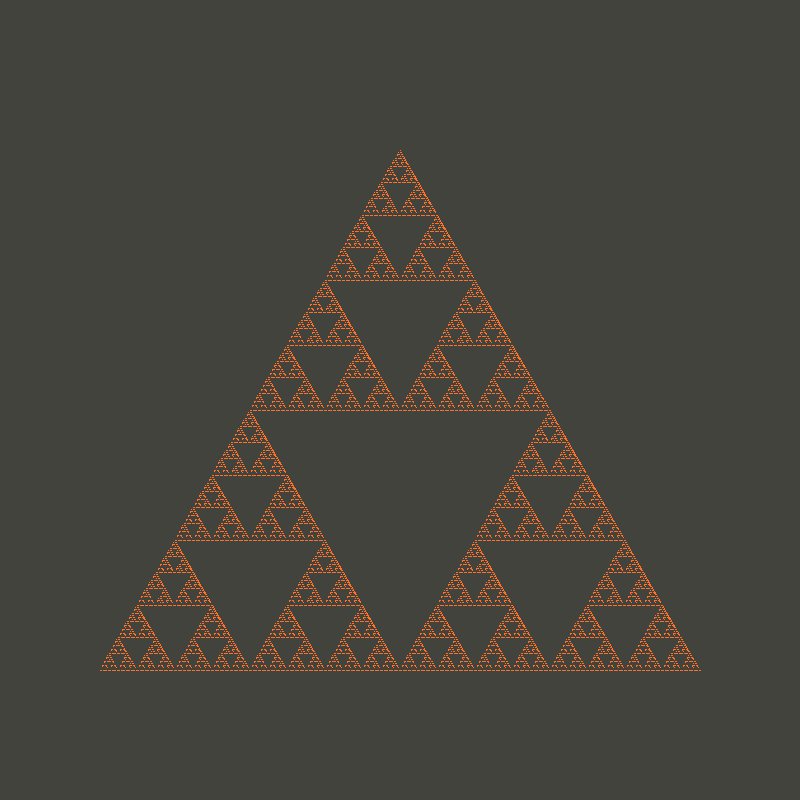
In this chapter, we will implement a function to draw the Sierpinski
Triangle, with the help of the pygame module. Here is the
header and docstring for our function:
import pygame
def sierpinski(screen: pygame.Surface, v0: tuple[int, int], v1: tuple[int, int],
v2: tuple[int, int]) -> None:
"""Draw a Sierpinski Triangle on the given screen, with the given vertices.
Each of v0, v1, and v2 is an (x, y) tuple representing a vertex of the triangle.
v0 is the lower-left vertex, v1 is the upper vertex, and v2 is the lower-right vertex.
"""The first function parameter, screen, is a
pygame.Surface object, which represents the surface on
which to draw this image. The other three parameters are \((x, y)\) coordinates that denote the
positions of the three vertices of the
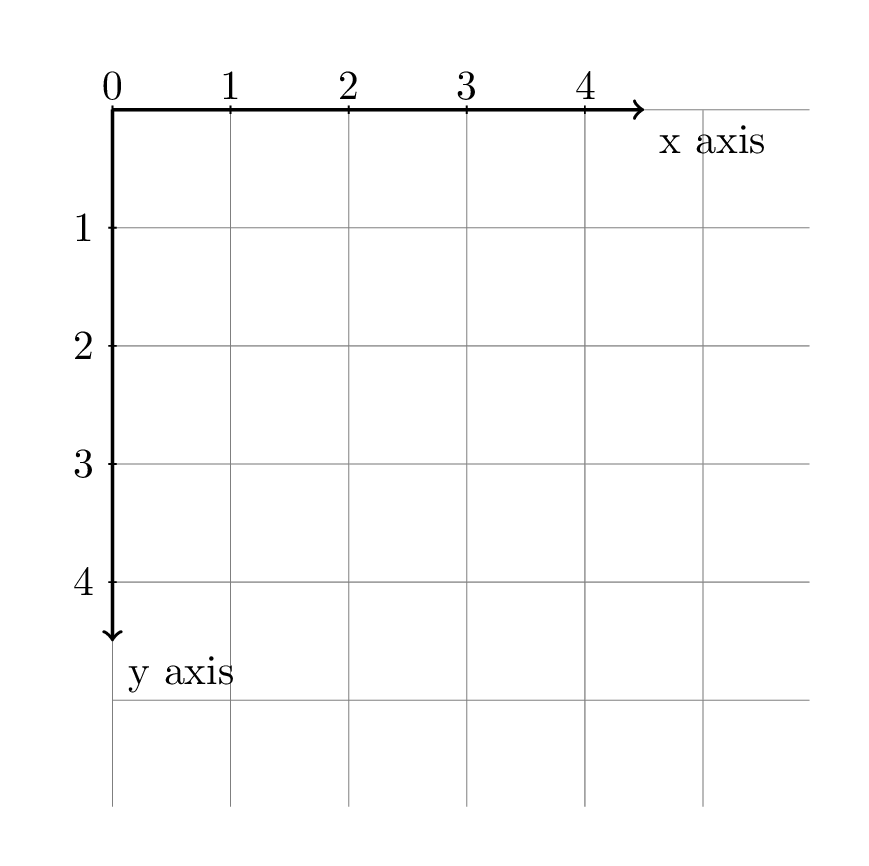
triangle. Note: The pygame coordinate
system may be different from what you are used to! With
pygame, the origin is located in the top left corner. The
positive \(x\)-axis extends to the
right and the positive \(y\)-axis
extends downwards.
Given the recursive nature of the Sierpinski Triangle, it is no
surprise that our function will be defined recursively. Before we begin
writing any code, we need to determine what value we will be recursing
on. This is more complex than either recursion with natural numbers or
the recursive data types we’ve studied previously in this chapter! Our
inputs here are the vertices of a triangle, so it’s not clear what
should “get smaller” at each successive recursive call to
sierpinski.
The key insight is that it is the triangle itself that gets smaller and smaller. More precisely, the side length of the triangle decreases by a factor of 2 at each call, since we use the midpoints of each side to form the smaller triangles.
Next, we should think about what the base case and the recursive step of our function should be.
Implementing the base case
In theory, the Sierpinski Triangle is recursively subdivided into smaller triangles an infinite number of times. However, there is no way to draw triangles that are “infinitely small” on a computer. So our base case instead will be when the triangle side length reaches a “small enough” value that we stop subdividing.
In our code, since we know v0 and v2 are
the lower-left and lower-right vertices of the triangle, we can use the
expression v2[0] - v0[0] to calculate the side length. But
how small is “small enough”? There is no definitive answer to this
question, so we’ll define a constant in our file that we can tweak
later.
MIN_SIDE = 3
def sierpinski(screen: pygame.Surface, v0: tuple[int, int], v1: tuple[int, int],
v2: tuple[int, int]) -> None:
"""..."""
if v2[0] - v0[0] < MIN_SIDE:
# Draw the triangle
pygame.draw.polygon(screen, (255, 113, 41), [v0, v1, v2])
else:
...Note that we use pygame.draw.polygon to draw the
triangle on the screen. (255, 113, 41) is the colour of our
triangle (represented as an RGB
tuple!), and the third argument is a list of vertices.
The recursive step
In the case that the triangle needs to be subdivided further, we first draw the triangle, as in our base case:
...
else:
pygame.draw.polygon(screen, (255, 113, 41), [v0, v1, v2])But we don’t stop there! Next, we need to determine the coordinates
of the vertices of the “sub-triangles” to draw. To do this, we implement
the helper function midpoint to help us calculate the
midpoint between two points.
def midpoint(p1: tuple[int, int], p2: tuple[int, int]) -> tuple[int, int]:
"""Return the midpoint of p1 and p2."""
return ((p1[0] + p2[0]) // 2, (p1[1] + p2[1]) // 2)And now we can use this function in our recursive step to calculate the midpoints of all three sides:
...
else:
pygame.draw.polygon(screen, (255, 113, 41), [v0, v1, v2])
mid0 = midpoint(v0, v1)
mid1 = midpoint(v0, v2)
mid2 = midpoint(v1, v2)The following diagram shows the coordinates of the vertices of the main triangle and sub-triangles.
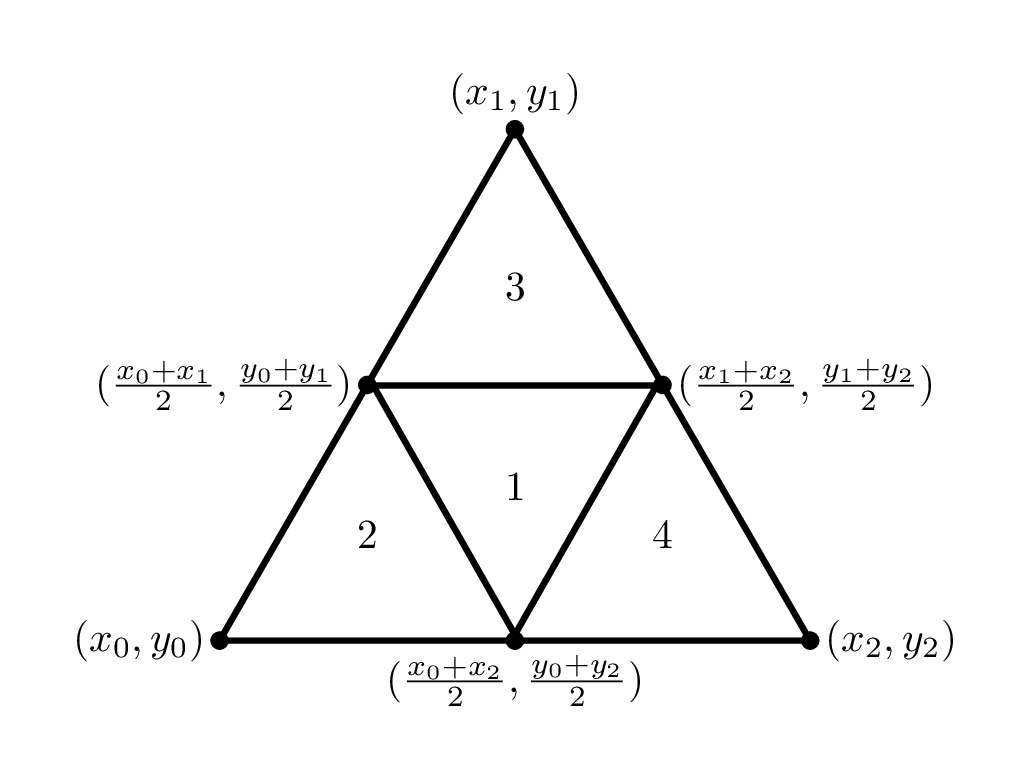
The next step is to fill the centre sub-triangle (labelled 1 in the diagram above) with “negative space”, a dark gray colour.
def sierpinski(screen: pygame.Surface, vertices: list[tuple[int, int]]) -> None:
...
else:
pygame.draw.polygon(screen, (255, 113, 41), [v0, v1, v2])
mid0 = midpoint(v0, v1)
mid1 = midpoint(v0, v2)
mid2 = midpoint(v1, v2)
# Draw centre "sub-triangle"
pygame.draw.polygon(screen, (46, 47, 41), [mid0, mid1, mid2])Lastly, the remaining three sub-triangles (labelled 2, 3, and 4)
should themselves be Sierpinski Triangles. We obtain their vertices from
the labelled diagram above and recursively call sierpinski
on each of them.
...
else:
pygame.draw.polygon(screen, (255, 113, 41), [v0, v1, v2])
mid0 = midpoint(v0, v1)
mid1 = midpoint(v0, v2)
mid2 = midpoint(v1, v2)
# Draw centre "sub-triangle"
pygame.draw.polygon(screen, (46, 47, 41), [mid0, mid1, mid2])
# Recursively draw other three "sub-triangles"
sierpinski(screen, v0, mid0, mid1)
sierpinski(screen, mid0, v1, mid2)
sierpinski(screen, mid1, mid2, v2)We can now set up a new pygame screen and call our
function in a main block. Here’s a complete version of our
code: In addition to the main block, we’ve pulled out the
colours into top-level constants to make it easier to tweak them
later.
import pygame
# Define some colours using their RGB values
FOREGROUND = (255, 113, 41)
BACKGROUND = (46, 47, 41)
# The minimum number of pixels in the Sierpinski triangle
MIN_SIDE = 3
def sierpinski(screen: pygame.Surface, v0: tuple[int, int], v1: tuple[int, int],
v2: tuple[int, int]) -> None:
"""Draw a Sierpinski Triangle on the given screen, with the given vertices.
Each of v0, v1, and v2 is an (x, y) tuple representing a vertex of the triangle.
v0 is the lower-left vertex, v1 is the upper vertex, and v2 is the lower-right vertex.
"""
if v2[0] - v0[0] < MIN_SIDE:
pygame.draw.polygon(screen, FOREGROUND, [v0, v1, v2])
else:
pygame.draw.polygon(screen, FOREGROUND, [v0, v1, v2])
mid0 = midpoint(v0, v1)
mid1 = midpoint(v0, v2)
mid2 = midpoint(v1, v2)
# Draw centre "sub-triangle"
pygame.draw.polygon(screen, BACKGROUND, [mid0, mid1, mid2])
# Recursively draw other three "sub-triangles"
sierpinski(screen, v0, mid0, mid1)
sierpinski(screen, mid0, v1, mid2)
sierpinski(screen, mid1, mid2, v2)
def midpoint(p1: tuple[int, int], p2: tuple[int, int]) -> tuple[int, int]:
"""Return the midpoint of p1 and p2."""
return ((p1[0] + p2[0]) // 2, (p1[1] + p2[1]) // 2)
if __name__ == '__main__':
# Initialize a pygame window
pygame.init()
window = pygame.display.set_mode((800, 800))
window.fill(BACKGROUND)
# Draw the Sierpinski Triangle!
sierpinski(window, (100, 670), (400, 150), (700, 670))
# Render the image to our screen
pygame.display.flip()
# Wait until the user closes the Pygame window
pygame.event.clear()
pygame.event.set_blocked(None)
pygame.event.set_allowed(pygame.QUIT)
pygame.event.wait()
pygame.quit()And please feel free to download sierpinski.py, which contains a slightly modified version that animates this drawing!
