10.8 Priority Queues

Not all lineups work the same way. While the lineup at a McDonald’s restaurant serves customers in a first-in-first-out order, the emergency room at a hospital does not see patients in the order that they arrive. Instead, the medical team perform an initial assessment of each patient for the severity of their illness, and patients with more life-threatening issues are seen earlier than others, regardless of when they arrived. In other words, patients are prioritized based on their condition.

The Priority Queue ADT

The Priority Queue ADT is similar to the Queue ADT, except that every item has some measure of its “priority”. Items are removed from a Priority Queue in order of their priority, and ties are broken in FIFO order. To summarize:

• Priority Queue
  • Data: a collection of items and their priorities
  • Operations: determine whether the priority queue is empty, add an item with a priority (enqueue), remove the highest priority item (dequeue)

One subtlety with our definition of this ADT is in how we represent priorities. For this section, we’ll simply represent priorities as integers, with larger integers representing higher priorities. In the next chapter, we’ll study an application of priority queues that uses a different way of representing priorities.

Here is the public interface of a PriorityQueue class.

from typing import Any


class PriorityQueue:
    """A collection items that are be removed in priority order.

    When removing an item from the queue, the highest-priority item is the one
    that is removed.

    >>> pq = PriorityQueue()
    >>> pq.is_empty()
    True
    >>> pq.enqueue(1, 'hello')
    >>> pq.is_empty()
    False
    >>> pq.enqueue(5, 'goodbye')
    >>> pq.enqueue(2, 'hi')
    >>> pq.dequeue()
    'goodbye'
    """

    def __init__(self) -> None:
        """Initialize a new and empty priority queue."""

    def is_empty(self) -> bool:
        """Return whether this priority queue contains no items.
        """

    def enqueue(self, priority: int, item: Any) -> None:
        """Add the given item with the given priority to this priority queue.
        """

    def dequeue(self) -> Any:
        """Remove and return the item with the highest priority.

        Raise an EmptyPriorityQueueError when the priority queue is empty.
        """


class EmptyPriorityQueueError(Exception):
    """Exception raised when calling pop on an empty priority queue."""

    def __str__(self) -> str:
        """Return a string representation of this error."""
        return 'You called dequeue on an empty priority queue.'

List-based implementation of the Priority Queue ADT

Unlike with the Stack and Queue ADTs, it is not clear if we can use a list here. Somehow we need to not only store items, but also keep track of which one has the largest priority, and in the case of ties, which one was inserted first.

Our implementation idea here is to use a private attribute that is a list of tuples, where each tuple is a (priority, item) pair. Our list will also be sorted with respect to priority (breaking ties by insertion order), so that the last element in the list is always the next item to be removed from the priority queue.

With this idea, three of the four PriorityQueue methods are straightforward to implement:

class PriorityQueue:
    """A queue of items that can be dequeued in priority order.

    When removing an item from the queue, the highest-priority item is the one
    that is removed.
    """
    # Private Instance Attributes:
    #   - _items: a list of the items in this priority queue
    _items: list[tuple[int, Any]]

    def __init__(self) -> None:
        """Initialize a new and empty priority queue."""
        self._items = []

    def is_empty(self) -> bool:
        """Return whether this priority queue contains no items.
        """
        return self._items == []

    def dequeue(self) -> Any:
        """Remove and return the item with the highest priority.

        Raise an EmptyPriorityQueueError when the priority queue is empty.
        """
        if self.is_empty():
            raise EmptyPriorityQueueError
        else:
            _priority, item = self._items.pop()
            return item

As an exercise, we’ll leave you to show that each of these operations runs in \(\Theta(1)\) time. But what about PriorityQueue.enqueue? An initial approach might be to first insert the new priority and item into the list, and then sort the list by priority. But this is a bit inefficient: we shouldn’t need to re-sort the entire list, if we start with a sorted list and are simply inserting one new item. We make this observation precise by observing that the worst-case running time of list.sort is \(\Theta(n \log n)\). We’ll study sorting algorithms in detail later on this year. 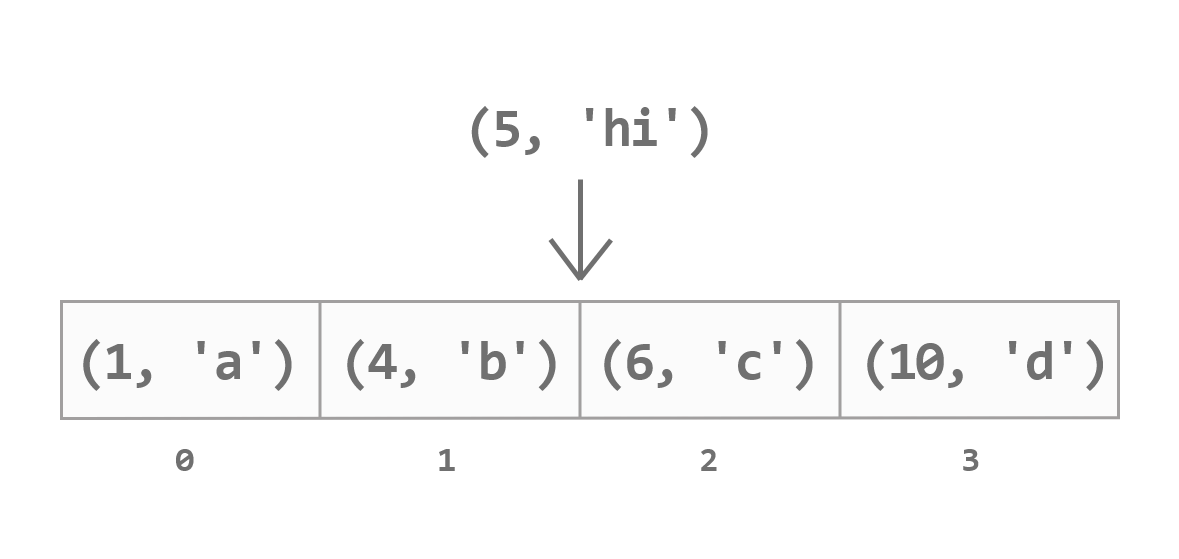So instead, our enqueue implementation will search for the right index in the list to add the new item. For example, suppose we want to insert the item 'hi' with priority 5 into the priority queue with self._items equal to [(1, 'a'), (4, 'b'), (6, 'c'), (10, 'd')]. We need to insert (5, 'hi') into index 2 in this list:

Here is our implementation of enqueue:

class PriorityQueue:
    ...

    def enqueue(self, priority: int, item: Any) -> None:
        """Add the given item with the given priority to this priority queue.
        """
        i = 0
        while i < len(self._items) and self._items[i][0] < priority:
            # Loop invariant: all items in self._items[0:i]
            # have a lower priority than <priority>.
            i = i + 1

        self._items.insert(i, (priority, item))

In the second part of the loop condition, you might wonder about the <: could we do self._items[i][0] <= priority instead? Does it make a difference? It turns out that switching < for <= in the second part of the condition does make a difference when it comes to breaking ties. We’ll leave it as an exercise for you to work this out: try tracing an enqueue operation for the item 'hi' with priority 5 into the priority queue with self._items equal to [(1, 'a'), (5, 'b'), (5, 'c'), (10, 'd')].

Running-time analysis

We’ll leave it as an exercise to show that the running times of our implementations of PriorityQueue.dequeue takes \(\Theta(1)\) time.

What about PriorityQueue.enqueue? The loop here is a bit tricky to analyze because the number of iterations is not a fixed number in terms of \(n\). Here is one preliminary analysis:

This might look good, but we made some approximations in this analysis: by using “at most”, we only obtained an upper bound on the running time, which is why our final result uses Big-O instead of Theta. It turns out that we can do better by incorporating the index i in our analysis.

By doing this more careful analysis, we no longer have an “at most” approximation, and so we’ve shown that every call to this implementation of PriorityQueue.enqueue will take \(\Theta(n)\) time, regardless of the priority being inserted.

Is there a better priority queue implementation?

Our implementation of PriorityQueue has a constant-time dequeue but a linear-time enqueue. You might naturally wonder if we can do better: what if we used an unsorted list of tuples instead? This would allow us to have \(\Theta(1)\) enqueue operations, simply by appending a new (priority, item) tuple to the end of self._items. However, we have simply shifted the work over to the dequeue operation. Specifically, we must search for the highest priority item in a list of unsorted items, which would take \(\Theta(n)\) time. Yet another trade-off!

In CSC263/CSC265, you’ll learn about the heap, a data structure which is commonly used in practice to implement the Priority Queue ADT. We can use this data structure to implement both PriorityQueue.enqueue and PriorityQueue.dequeue with a worst-case running time of \(\Theta(\log n)\). This is actually the approach taken by Python’s built-in heapq module. Pretty neat!