\( \newcommand{\NOT}{\neg} \newcommand{\AND}{\wedge} \newcommand{\OR}{\vee} \newcommand{\XOR}{\oplus} \newcommand{\IMP}{\Rightarrow} \newcommand{\IFF}{\Leftrightarrow} \newcommand{\TRUE}{\text{True}\xspace} \newcommand{\FALSE}{\text{False}\xspace} \newcommand{\IN}{\,{\in}\,} \newcommand{\NOTIN}{\,{\notin}\,} \newcommand{\TO}{\rightarrow} \newcommand{\DIV}{\mid} \newcommand{\NDIV}{\nmid} \newcommand{\MOD}[1]{\pmod{#1}} \newcommand{\MODS}[1]{\ (\text{mod}\ #1)} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R} \newcommand{\C}{\mathbb C} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cL}{\mathcal L} \newcommand{\cK}{\mathcal K} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cZ}{\mathcal Z} \newcommand{\emp}{\emptyset} \newcommand{\bs}{\backslash} \newcommand{\floor}[1]{\left \lfloor #1 \right \rfloor} \newcommand{\ceil}[1]{\left \lceil #1 \right \rceil} \newcommand{\abs}[1]{\left | #1 \right |} \newcommand{\xspace}{} \newcommand{\proofheader}[1]{\underline{\textbf{#1}}} \)

8.3 Computing Shared Secret Keys

A historical limitation of symmetric-key cryptosystems was how to establish a shared, but secret, key. If the two communicating parties were able to meet in person, they could agree upon a shared secret key while physically together (assuming no one else was spying on them). But what if I want to communicate with someone securely in a different city or different country? Or—to use a more modern example—to communicate with a server across the Internet, which I cannot hope to meet in person?

One solution to this problem is the Diffie-Hellman key exchange, which is an algorithm that is executed by two people (or computers) to compute a shared secret, while communicating in public (open to eavesdroppers). We will introduce the intuitions of the Diffie-Hellman key exchange with an analogy that uses our familiar Alice and Bob communicating with colours. After, we will replace colours with numbers to understand how the process works in today’s digital world.

Alice and Bob are mixing paint

Suppose that Alice and Bob would like to establish a secret paint colour that only the two of them know. They use the following procedure.

First, they both agree on a random, not-secret colour of paint to start with: yellow. They decide on this shared colour publicly, so eavesdroppers also know this colour!

Second, they each choose their own secret colour, which they will never share with each other or anyone else. In our example, Alice decides on red and Bob chooses teal (a green-blue colour).

Third, they each mix their secret colours with their shared colour yellow, producing a light orange for Alice and a blue for Bob. This is also done in secret.

Fourth, they exchange these colours with each other, which is done publicly. At this point, there are three not-secret colours: yellow and the two mixtures. And there are two secret colours: Alice’s red and Bob’s teal.

Fifth, Alice mixes Bob’s blue colour with her original secret red to produce a brown. Bob mixes Alice’s light orange with his original secret teal to produce the same brown. Why are these the same brown? Because they both consist of the same mixture of three colours: yellow (shared), red (Alice’s secret), and teal (Bob’s secret)!

Finally, why is this brown a secret? Any eavesdropper has access to three colours: the original shared yellow (from the first step), and the two mixtures orange and blue (from the fourth step). If we assume that the colour mixtures are not easily separated (i.e., it is very difficult to extract the yellow from each mixture), then the eavesdropper cannot determine what Alice and Bob’s secret colours were, and therefore can’t mix them together with the yellow to produce the right shade of brown!
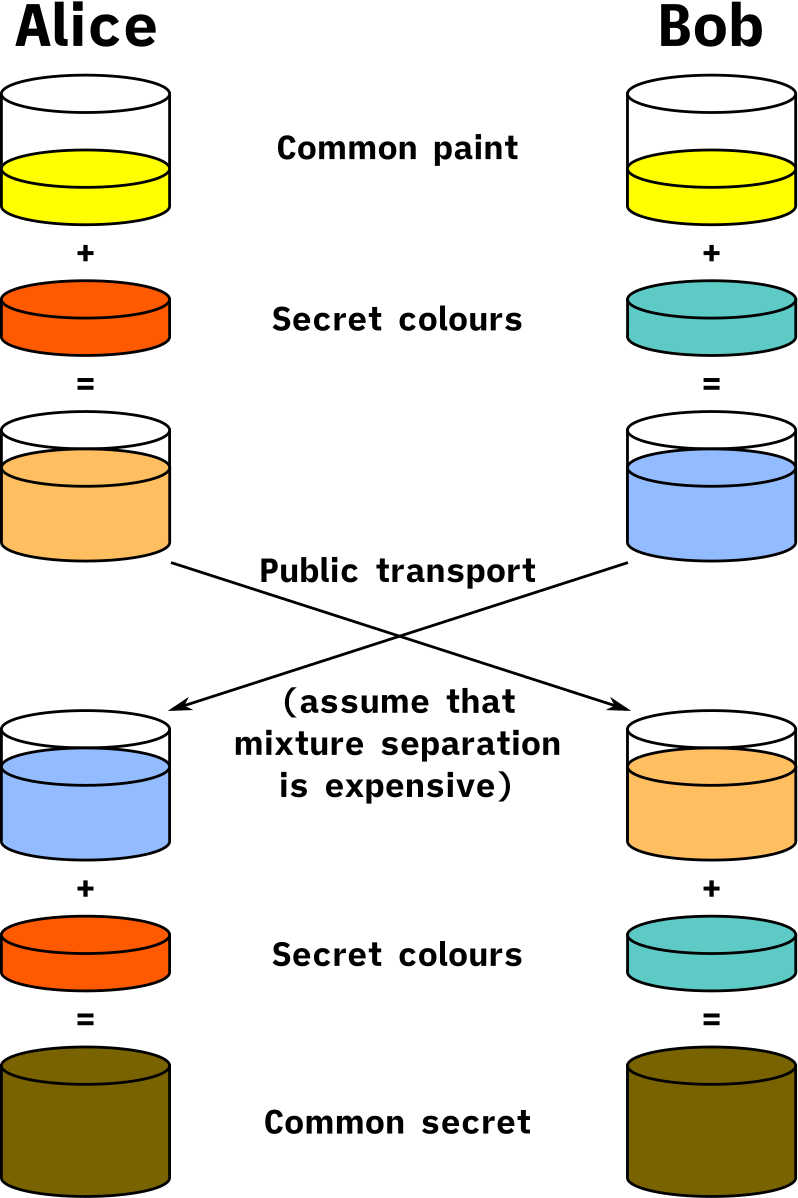
Image from https://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange

The Diffie-Hellman key exchange

Unfortunately, transmitting paint across digital channels is intractable, but transmitting numbers isn’t. The Diffie-Hellman key exchange uses some neat (yet simple) operations from modular arithmetic to play out the same scenario as our paint analogy.

Diffie-Hellman Key Exchange Algorithm

Setting: Two parties, Alice and Bob.

Result: Alice and Bob share a secret key \(k\).

  1. Alice chooses a prime number \(p\) greater than two and an integer \(g\) such that \(2 \leq g \leq p - 1\), and sends both numbers \((p, g)\) to Bob.

  2. Alice chooses a secret number \(a \in \{1, 2, \dots, p-1\}\) and sends Bob \(A = g^a ~\%~ p\) to Bob.

  3. Bob chooses a secret number \(b \in \{1, 2, \dots, p-1\}\) and sends \(B = g^b ~\%~ p\) to Alice.

  4. Alice computes \(k_A = B^a ~\%~ p\). Bob computes \(k_B = A^b ~\%~ p\).

    Then \(k_A = k_B\), and so this value is the secret key \(k\) that Alice and Bob share.

An example

Here is an example of the Diffie-Hellman key exchange in action.

  1. Alice starts by choosing \(p = 23\) and \(g = 2\). She sends both \(p\) and \(g\) to Bob.
  2. Alice chooses a secret number \(a = 5\). She sends \(A = g^a ~\%~ p = 2^5 ~\%~ 23 = 9\) to Bob.
  3. Bob chooses a secret number \(b = 14\). He sends \(B = g^b ~\%~ p = 2^{14} ~\%~ 23 = 8\) to Alice.
  4. Alice computes \(k_A = B^a ~\%~ p = 8^5 ~\%~ 23 = 16\). Bob computes \(k_B = A^b ~\%~ p = 9^{14} ~\%~ 23 = 16\). As expected, \(k_A = k_B\), and these form the secret key \(k\)!

Correctness: Are \(k_A\) and \(k_B\) always equal?

That last sentence in the Diffie-Hellman key exchange algorithm description is doing a lot of work. How do we “know” that \(k_A = k_B\)? With a proof, of course!

(Correctness of Diffie-Hellman key exchange)

For all \(p, g, a, b \in \Z^+\), \((g^b ~\%~ p)^a ~\%~ p = (g^a ~\%~ p)^b ~\%~ p\).

Even though the Diffie-Hellman algorithm frames the communication in terms of remainders, we can analyze the numbers using modular arithmetic modulo \(p\). In this case the calculation involves just switching around exponents in \(g^{ab}\).

Let \(p, g, a, b \in \Z^+\). Let \(A = g^a ~\%~ p\) and \(B = g^b ~\%~ p\). We’ll prove that \(B^a ~\%~ p = A^b ~\%~ p\).

First, we have that \(A \equiv g^a \pmod p\) and \(B \equiv g^b \pmod p\). So then \(A^b \equiv (g^a)^b \equiv g^{ab} \pmod p\), and \(B^a \equiv (g^b)^a \equiv g^{ba} \pmod p\).

Since \(g^{ab} = g^{ba}\), we can conclude that \(A^b \equiv B^a \pmod p\).

So then \(A^b\) and \(B^a\) must have the same remainder when divided by \(p\), and so \(B^a ~\%~ p = A^b ~\%~ p\).

Security: How secret is the key?

We’ve just proved that the Diffie-Hellman key exchange is correct, meaning the result at the end of the algorithm is that Alice and Bob have a shared key. But that’s not the only purpose of this algorithm: it must also ensure that this shared key is also secret, unknown to anyone other than Alice and Bob.

So let’s look at the Diffie-Hellman key exchange from the perspective of an eavesdropper that has access to everything Alice and Bob communicate to each other. We say that Alice and Bob’s communications are public, while their own computing devices are private. So over the course of the algorithm, the eavesdropper has access to \(p\), \(g\), \(g^a ~\%~ p\), and \(g^b ~\%~ p\). The question is: from this information, can the eavesdropper determine the secret key \(k\)?

One approach an eavesdropper could take is to try to compute \(a\) and \(b\) directly. This is an instance of the discrete logarithm problem: given \(p, g, y \in \Z^+\), find an \(x \in \N\) such that \(g^x \equiv y \pmod p\). While we could implement a brute-force algorithm for solving this problem that simply tries all possible exponents \(x \in \{0, 1, \dots, p-1\}\), this is computationally inefficient in practice when \(p\) is chosen to be extremely large. We’ll explore exactly what we mean by terms like “efficient” and “inefficient” more precisely in the next chapter.

Perhaps surprisingly, there is no known efficient algorithm for solving the discrete logarithm problem! So we say that the Diffie-Hellman key exchange is computationally secure: while there are known algorithms that eavesdroppers could use for determining the shared secret key, all known algorithms are computationally infeasible for standard primes chosen. In practice, Diffie-Hellman key exchanges tend to use primes on the order of \(2^{2048} \approx 10^{617}\), or in other words prime numbers with over 600 digits!