\( \newcommand{\NOT}{\neg} \newcommand{\AND}{\wedge} \newcommand{\OR}{\vee} \newcommand{\XOR}{\oplus} \newcommand{\IMP}{\Rightarrow} \newcommand{\IFF}{\Leftrightarrow} \newcommand{\TRUE}{\text{True}\xspace} \newcommand{\FALSE}{\text{False}\xspace} \newcommand{\IN}{\,{\in}\,} \newcommand{\NOTIN}{\,{\notin}\,} \newcommand{\TO}{\rightarrow} \newcommand{\DIV}{\mid} \newcommand{\NDIV}{\nmid} \newcommand{\MOD}[1]{\pmod{#1}} \newcommand{\MODS}[1]{\ (\text{mod}\ #1)} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R} \newcommand{\C}{\mathbb C} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cL}{\mathcal L} \newcommand{\cK}{\mathcal K} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cZ}{\mathcal Z} \newcommand{\emp}{\emptyset} \newcommand{\bs}{\backslash} \newcommand{\floor}[1]{\left \lfloor #1 \right \rfloor} \newcommand{\ceil}[1]{\left \lceil #1 \right \rceil} \newcommand{\abs}[1]{\left | #1 \right |} \newcommand{\xspace}{} \newcommand{\proofheader}[1]{\underline{\textbf{#1}}} \)

8.2 The One-Time Pad and Perfect Secrecy

The Caesar cipher we studied in the previous section is simple enough as a starting point, but should never be used in practice! It suffers from the fatal flaw that each character of the plaintext is encrypted individually, using the same secret key each time. So for example, every occurrence of the character 'D' in the plaintext is transformed into the same character in the ciphertext. Why is this a problem?

Consider the ciphertext 'OLaTO+T^+NZZW' generated by the ASCII-based Caesar cipher. Even though it may look indecipherable at first, there is information that we can learn about the original plaintext just by looking at the distribution of letters in the ciphertext. Given these observations and the hint that the plaintext is a common phrase used in CSC110, can you determine the plaintext?

In addition to what we can infer from the distribution of letters in the ciphertext, the ASCII-based Caesar cipher is vulnerable to a brute-force exhaustive key search attack. There are only 127 possible secret keys the cipher could use (corresponding to the possible non-zero remainders when dividing by 128). So, given a ciphertext, it is possible to try out every secret key and see which key yields a meaningful plaintext message. For most ciphertexts generated from English plaintexts, only one possible secret key causes the decrypted message to be a meaningful English message. That’s not very secure.

Even if we enlarge the set of possible keys (e.g., by using a more general text encoding like UTF8), Caesar ciphers are still vulnerable to observations like the ones we made earlier. From these observations, we can identify “likely” keys that a brute force search could try first. So the main weakness of the Caesar cipher is not just the number of possible keys.

The one-time pad

We will now introduce a new symmetric-key cryptosystem known as the one-time pad that is structurally similar to the Caesar cipher, but avoids the issues we raised earlier. Encryption in the one-time pad works by shifting each character in the plaintext message, much like the Caesar cipher. But where the one-time pad differs is that the shift is not the same for each character. The one-time pad accomplishes this by not using a single number for the secret key, but rather a string of length greater than or equal to the length of the plaintext message you wish to encrypt. This secret key is colloquially referred to as a “one-time pad” (of characters), from which this cryptosystem gets its name.

To encrypt a plaintext ASCII message \(m\) with secret key \(k\), for each index \(i\) between 0 and \(|m| - 1\), we compute:

Here is an example. Suppose we wanted to encrypt the plaintext 'HELLO' with the secret key 'david'. The ciphertext will have five characters, where the first is 'H' + 'd' which results in ',', the second is 'E' + 'a' which results in '&', etc. The following diagram shows the full conversion:

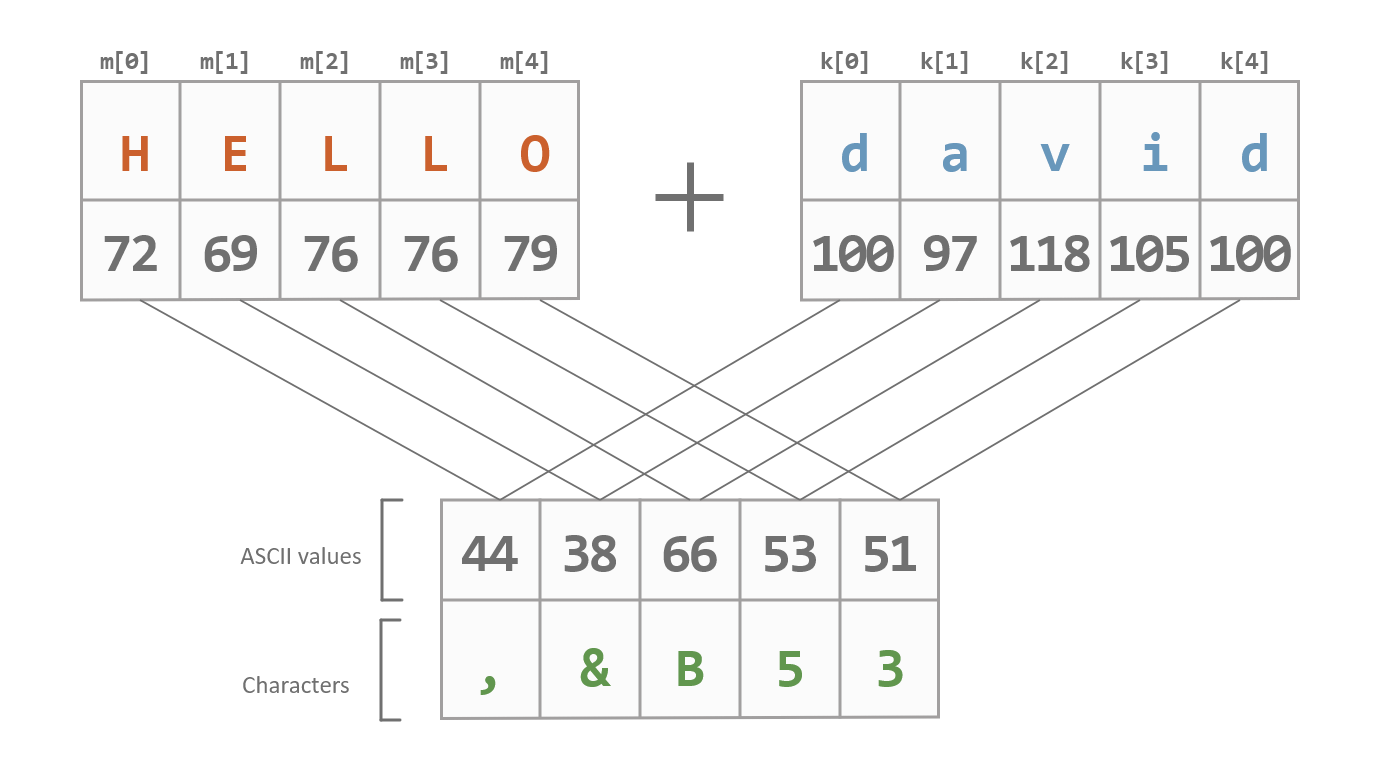
One-Time Pad Example Diagram

Similarly, for decryption we take the ciphertext c and recover the plaintext by subtracting each letter of the secret key: \((c[i] - k[i]) ~\%~ 128\).

Perfect secrecy and its costs

The one-time pad cryptosystem is famous in cryptography for having a property known as perfect secrecy, This is a term coined by the mathematician and cryptographer Claude Shannon in 1949. which informally means that a ciphertext reveals no information about its corresponding plaintext other than its length. To see why, take our previous example, with ciphertext ',&B53'. This ciphertext could have been generated by any five-letter plaintext message, because for any such message there exists a secret key that could encrypt that message to obtain ',&B53'. The sender could have been sending plaintext message 'HELLO' with secret key 'david', but it is equally likely they could have been sending the message 'FUNNY' with secret key 'fQtgZ'. Because of perfect secrecy, an eavesdropper cannot gain any information about the original plaintext message, even if they know the whole ciphertext.

This perfect secrecy comes at a cost, however. The main drawback of the one-time pad cryptosystem, and why it is not actually used in practice, is that the secret key must have at least the same length as the message being sent, and cannot be reused from one message to another. The notion of perfect secrecy relies on every possible secret key to be chosen purely at random. This isn’t the case if I reuse the same one-time pad for all my messages. This requirement is also why the term “one-time” is used for one-time pads.

Stream ciphers

The attraction of perfect secrecy has led cryptographers to develop stream ciphers, which are a type of symmetric-key cryptosystem that emulate a one-time pad but share a much smaller secret key. The details of stream ciphers are beyond the scope of this course, but the basic is idea is the following: the shared secret key is quite small, and both parties use an algorithm to generate an arbitrary number of new random characters, based on both the secret key and any previously-generated characters. We say that this is a “stream” of characters, from which this type of cryptosystem gets its name. These characters are then used in the same way as a one-time pad to encrypt messages.

Now, stream ciphers do not have perfect secrecy, since the characters used in encryption aren’t truly random. But if the generating algorithm is clever enough, each new character appears “random”, and the encrypted messages are computationally impossible to decrypt without knowing the starting secret key. In other words, stream ciphers give up on perfect secrecy in exchange for “good enough” secrecy and a much, much smaller shared secret key. Of course, the “good enough” is highly dependent on the algorithm used to generate the characters. A poorly-designed algorithm may unintentionally inject patterns in the generated characters, or even allow an eavesdropper to gain some information about the secret key itself!