CSC411/2515 Project 1: Face Recognition and Gender Classification with Regression

For this project, you will build a system for face recognition and gender classification, and test it on a large(-ish) dataset of faces, getting practice with data-science-flavour projects along the way. You may import things like numpy and matplotlib, but the idea is to implement things “from scratch”: you may not import libraries that will do your work for you!

The input

You will work with a subset of the FaceScrub dataset. The subset of male actors is here and the subset of female actors is here. The dataset consists of URLs of images with faces, as well as the bounding boxes of the faces. The format of the bounding box is as follows (from the FaceScrub readme.txt file):

The format is x1,y1,x2,y2, where (x1,y1) is the coordinate of the top-left corner of the bounding box and (x2,y2) is that of the bottom-right corner, with (0,0) as the top-left corner of the image. Assuming the image is represented as a Python NumPy array I, a face in I can be obtained as I[y1:y2, x1:x2].

You may find it helpful to use a modified version of our script for downloading the image data. (Note that the script is not meant to be used as is. You need to figure out how to modify it.)

At first, you should work with the faces of the following actors:

    act =['Lorraine Bracco', 'Peri Gilpin', 'Angie Harmon', 'Alec Baldwin', 'Bill Hader', 'Steve Carell']

For this project, you should crop out the images of the faces, convert them to grayscale, and resize them to 32x32 before proceeding further. You can use scipy.misc.imresize to scale images, and you can use rgb2gray to convert RGB images to grayscale images.

Part 1 (10%)

Describe the dataset of faces. In particular, provide at least three examples of the images in the dataset, as well as at least three examples of cropped out faces. Comment on the quality of the annotation of the dataset: are the bounding boxes accurate? Can the cropped-out faces be aligned with each other?

Part 2 (5%)

Separate the dataset into three non-overlapping parts: the training set (100 UPDATE: 70 face images per actor), the validation set (10 face images per actor), and the test set (10 face images per actor). For the report, describe the algorithm that you used to do that (any algorithm is fine, but you should use code to split up your dataset). The training set will contain faces whose labels you assume you know. The test set and the validation set will contain faces whose labels you pretend to not know and will attempt to determine using the data in the training set.

Part 3 (10%)

Use Linear Regression in order to build a classifier to distinguish pictures of Alec Baldwin form pictures of Steve Carell. In your report, specify which cost function you minimized. Report the values of the cost function on the training and the validation sets. Report the performance of the classifier (i.e., the percentage of images that were correctly classified) on the training and the validation sets.

You should use Gradient Descent in order to find the parameters \(\theta\).

In your report, include the code of the function that you used to compute the output of the classifier (i.e., either Steve Carell or Alec Baldwin).

In your report, describe what you had to do in order to get the system to work. For example, the system would not work if the parameter \(\alpha\) is too large. Describe what happens if \(\alpha\) is too large, and how you figure out what to set \(\alpha\) to. Describe the other choices that you made in order to make the algorithm work.

Tip: divide the input images by \(255.0\) so that all inputs are in the \(0...1\) range.

Part 4 (a) (7%)

In Part 3, you used the hypothesis function \(h_\theta (x) = \theta_0 + \theta_1 x_1 + ... + \theta_n x_n\). If \((x_1, ..., x_n)\) represents a flattened image, then \((\theta_1, ..., \theta_n)\) can also be viewed as an image. Display the \(\theta\)s that you obtain by training using the full training dataset, and by training using a training set that contains only two images of each actor.

The images could look as follows.

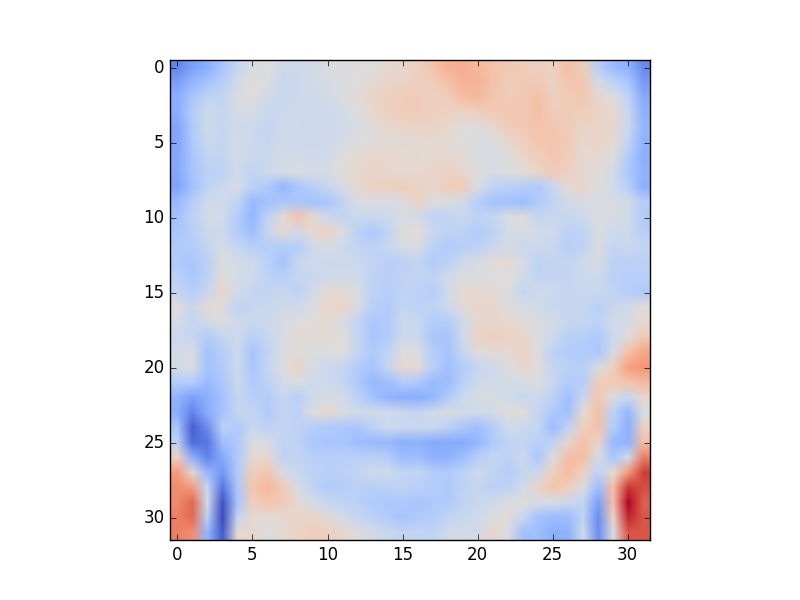
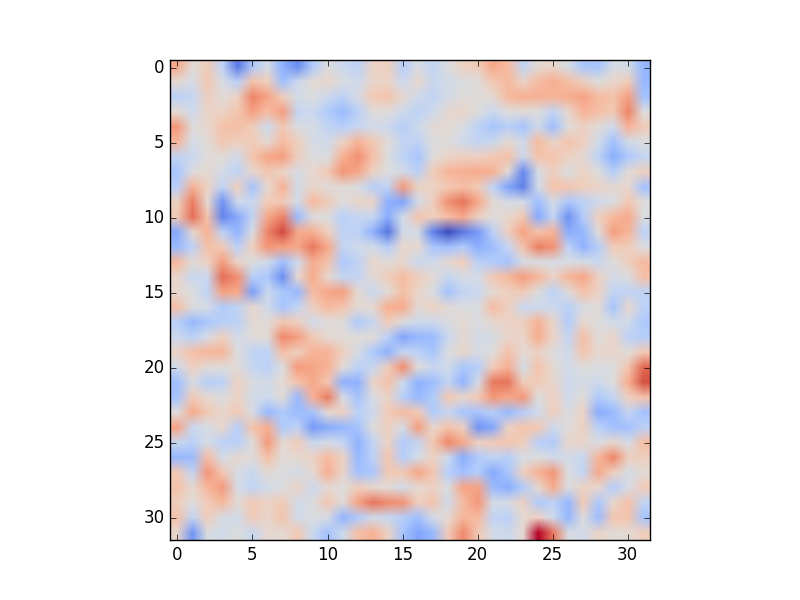
Part 4 (b) (3%)

In Part 4(a), you need to display whatever image Gradient Descent produced. In this part, you should experiment in order to produce both kinds of visualizations. Report on how to obtain both a visualization that contains a face and a visualization that does not, using the full training set. Be specific about what you did. Hint: try stopping the Gradient Descent process earlier and later in the process. Try initializing the \(\theta\)s using different strategies.

Part 5 (15%)

In this part, you will demonstrate overfitting. Build classifiers that classify the actors as male or female using the training set with the actors from

    act =['Lorraine Bracco', 'Peri Gilpin', 'Angie Harmon', 'Alec Baldwin', 'Bill Hader', 'Steve Carell']

and using training sets of various sizes. Plot the performance of the classifiers on the training and validation sets vs the size of the training set.

Report the performance of the classifier on 6 actors who are not included in act.

Part 6 (30%)

Now, consider a different way of classifying inputs. Instead of assigning the output value \(y=1\) to images of Paul McCartney and the output value \(y = -1\) to images of John Lennon, which would not generalize to more than 2 labels, we could assign output values as follows:

    Paul McCartney:     [1, 0, 0, 0]
    John Lennon:        [0, 1, 0, 0]
    George Harrison:    [0, 0, 1, 0]
    Ringo Starr:        [0, 0, 0, 1]
    

The output could still be computed using \(\theta^T x\), but \(\theta\) would now have to be a \(n\times k\) matrix, where \(k\) is the number of possible labels, with \(x\) being a \(n\times 1\) vector.

The cost function would still be the sum of squared differences between the expected outputs and the actual outputs:

\[J(\theta) = \sum_i (\sum_j (\theta^T x^{(i)}-y^{(i)})_j^{2}).\]

Part 6(a) (5%)

Compute \(\frac{\partial J}{\partial \theta_{pq}}\) . Show your work. Images of neatly hand-written derivations are acceptable, though you are encouraged to use LaTeX.

Part 6(b) (10%)

Show, by referring to Part 6(a), that the derivative of \(J(\theta)\) with respect to all the components of \(\theta\) can be written in matrix form as

\[2 X (\theta^T X-Y)^T .\]

Specify the dimensions of each matrix that you are using, and define each variable (e.g., we defined \(m\) as the number of training examples.) \(X\) is a matrix that contains all the input training data (and additional 1’s), of the appropriate dimensions.

Part 6(c) (5%)

Implement the cost function from Part 6(a) and its vectorized gradient function in Python. Include the code in your report.

Part 6(d) (10%)

Demonstrate that the vectorized gradient function works by computing several components of the gradient using finite-difference approximations. In your report, include the code that you used to compute the gradient components using finite differences, and to compare them to the gradient that you computed using your function. In one or two sentences, explain how you compared the approximated values to the output of the gradient function.

Recall that to compute a derivative of a 1-d function using a finite-difference approximation, you can use

\[f'(x) \approx \frac{f(x+h)-f(x)}{h}\]

for a small \(h\).

This can be generalized to functions of several variables.

In your report, explain how you selected an \(h\) that makes sense, It is enough to compute the finite-difference approximation along 5 coordinates (as long as the partial derivatives along those coordinates aren’t all 0).

The usual practice is to run the optimization for a while and then perform gradient checking. However, you do not have to do that for this project.

Part 7 (10%)

Run gradient descent on the set of six actors act in order to perform face recognition. Report the performance (i.e., proportion of correctly-classified faces) you obtained on the training and validation sets. Indicate what parameters you chose for gradient descent and why they seem to make sense. Describe how you obtained the label from the output of the model.

Part 8 (10%)

Visualize the \(\theta\)s that you obtained. Note that if \(\theta\) is a \(k\times n\) matrix, where \(k\) is the number of possible labels and \(n-1\) is the number of pixels in each image, the rows of \(\theta\) could be visualized as images. Your outputs could look something like the ones below. Label the images with the appropriate actor names.

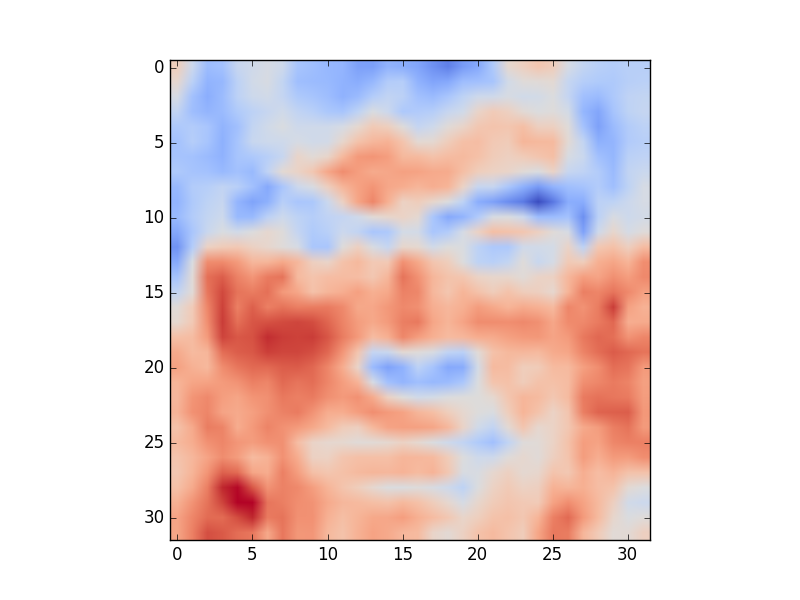
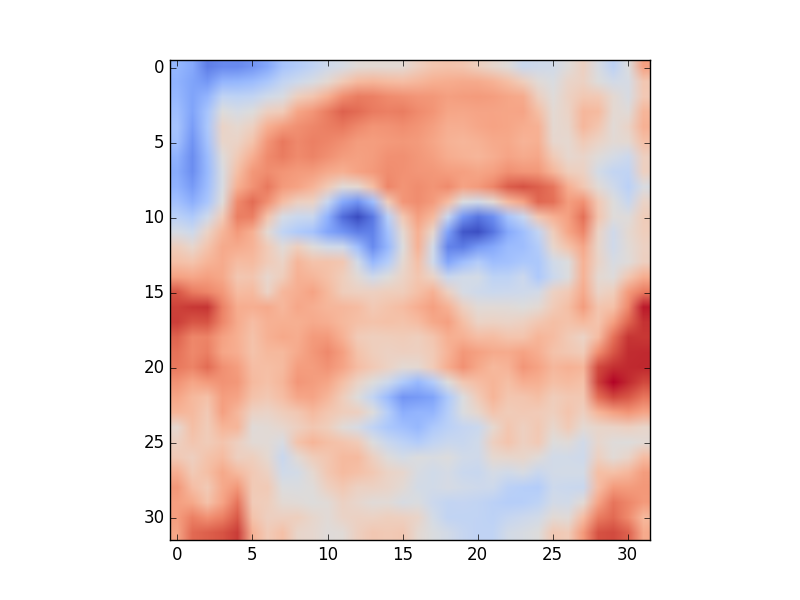
What to submit

The project should be implemented using Python 2 and should be runnable on the CS Teaching Labs computers. If you choose to deviate from that, state your system configuration clearly in your report so that we can reproduce your work if needed.

Your report should be in PDF format. You should use LaTeX to generate the report, and submit the .tex file as well. A sample template is on the course website. You will submit at least three files: faces.py, faces.tex, and faces.pdf. You may submit additional Python files if necessary.

Reproducibility counts! We should be able to obtain all the graphs and figures in your report by running your code. The only exception is that you may pre-download the images (what and how you did that, including the code you used to download the images, should be included in your submission.) Submissions that are not reproducible will not receive full marks. If your graphs/reported numbers cannot be reproduced by running the code, you may be docked up to 20%. (Of course, if the code is simply incomplete, you may lose even more.) Suggestion: if you are using randomness anywhere, use numpy.random.seed().

You must use LaTeX to generate the report. LaTeX is the tool used to generate virtually all technical reports and research papers in machine learning, and students report that after they get used to writing reports in LaTeX, they start using LaTeX for all their course reports. In addition, using LaTeX facilitates the production of reproducible results.

Using our code

You are free to use any of the code available from the CSC411/CSC2515 course website.

Readability

Readability counts! If your code isn’t readable or your report doesn’t make sense, they are not that useful. In addition, the TA can’t read them. You will lose marks for those things.

Academic integrity

It is perfectly fine to discuss general ideas with other people, if you acknowledge ideas in your report that are not your own. However, you must not look at other people’s code, or show your code to other people, and you must not look at other people’s reports and derivations, or show your report and derivations to other people. All of those things are academic offences.